How steep was my valley
Unclenching, Part 5.1
So far all our explorations in this series orbit something big: the tendency of living systems to lean into their behaviour to make it more robust to unpredicted forces which might interfere. The results are double-edged: behaviour that’s more locally robust is more likely to succeed in the presence of interference, but it’s also more likely to cling to power when something better might ought to replace it.
Where living things appear, so does robustening. And as is typical of inevitable human phenomena, people have described robustening many times before, more or less implicitly. In this series we’ve already seen it in the context of muscle clenching, self-fulfilling prophecies, and predictive coding. We’ve talked about the tradeoff between stubbornness and science—what it means to give structure out, versus take it in. We’ve also discussed some practices that people use to try to escape from harmfully robust mental states.
Now let’s elevate those earlier discussions with some ideas about dynamics, optimization, and brains.
We’ll pass arbitrarily close to the free energy principle. Some might say it’s what I’ve been talking about, all along. But literally everything is about the free energy principle, according to the free energy principle. More and more I’m stealing its language and ideas, but we won’t be focusing on it, this time.
This post is for those of us who are still beginning to understand.1
Everything changes — before too long, we should assume.
Sometimes a process changes slowly enough that we can treat it as though it is composed of some stable things or objects or parts. How long will the assumptions remain valid, that allow us to distinguish those parts? Perhaps things won’t change so much and so soon as to undermine our effort, and we’ll gain a little understanding before we’re forced to try again.2
A dynamical system is a precise, formal way of describing change over time. A classic example of dynamics is the movement of a pendulum, which swings back and forth under the influence of gravity. A simple pendulum is an easy thing to model as a dynamical system.
A complex system is a way of describing many parts that interact with each other. Out of all their local interactions, coherent behaviour can emerge. Individual birds in a flock make decisions that may be quite short-sighted, or local — something like follow the average direction of your neighbours. When many individuals get together and follow such a local rule, their movements cohere into flocking. They don’t scatter in random directions; something larger emerges from all the individuals. And no single bird has to ponder the flock as a whole, for the flock to behave as something like a superorganism3.
We can treat a flock as a dynamical system, with birds as its parts — its stable parts, which we assume aren’t doing much transforming into not-birds so long as we’re asking our questions.
We can describe the flock’s movement over time as a path through a state space. A single point in a system’s state space tells us the state of all that system's parts at a point in time. While the relevant state of an individual bird might be its current location, heading, and speed, a point in the flock’s state space gives us that information for every bird in the flock. Then a sequence of points forms a path, describing how the entire flock moves over time.

We can also treat a brain as a dynamical system. A brain isn’t made of birds: its parts are conventionally taken to be cells — specifically neurons. The state of each individual neuron might be its firing rate — how many times it emits an electrical discharge, every second. Then a single point in a brain’s state space represents all its neurons’ firing rates at once, and a path through the state space gives the history of firing rates for all the neurons over a given period of time.4

Maybe this all seems a bit too simple. A bird isn’t just a location, speed, and heading — actually it has its own brain full of neurons which effect its movements. And as it flies around, its muscles get tired and start to respond differently to the commands from its brain. There are many other bird-variables which might start mattering, depending on the questions we want to ask.
Similarly, a real neuron isn’t just some formless drum machine that pulses at a given rate, which we can summarize with a single number that changes over time. It’s much more complex. It has shape, metabolism, and a lot of other structure that isn’t captured by “firing”. Besides, neurons aren’t the only kind of cell in my brain.
We can wonder, how do researchers decide which variables, terms, or properties5 are important enough to include in their simplified models of a brain, or a neuron, or a bird? This question is related to whether the chosen parts of a system can be treated as stable enough to be modeled as such. It’s a very important question, but let’s leave it aside for now. Pretend it's just neurons and firing rates.6
Like birds, neurons don't act in just any way, to effect the larger whole of behaviour. To form a flock, birds don’t scatter in random directions. Likewise, my neurons don’t fire independently of each other. They don't follow just any path in state space, but something a little more ordered. Though each neuron acts locally, like a short-sighted bird, order arises because the neurons and their neighbours follow something almost like a rule — something like fire if enough of the neurons connected to me are firing.
The actual “rule” is more complex, though. A typical neuron has many other neurons connected to it, influencing it. It doesn’t listen to all of them equally. It doesn’t start its life with a grown-up balance of all those incoming influences. And it’s only one of many millions of neurons that needs to solve its own local variation of this problem, for useful order to arise.
Yet the neurons do learn to move together — to change all their local balances, to collectively form coherent patterns that effect how an animal acts in the world.
Learning means 1) deciding how well I’m achieving a goal, and 2) changing myself to better achieve it.
Looking at my brain as a dynamical system made of neurons, changing myself looks like adjusting the contracts — the strength of the influences — between neurons.
Of course I am not directly aware of the little adjustments that occur inside my brain as I learn. But that’s unnecessary, given that “I” operates at the level of goals, while the full machinery of my brain works out the little details. Neuron A starts listening to neuron B more than neuron C, and my behaviour changes very slightly. If enough of the right neurons adjust themselves, maybe I reach my goal a little better than I did last time.
And what about deciding how well I’m achieving my goal? Back in preschool, excited to reach for my favourite toy, I wished I would arrive in a definite state: I’ve grasped the toy in my hand. When we know exactly what my task is, we can use a loss function to describe how well I’m achieving it — precisely, explicitly, with math.
A loss function is just a way of keeping score. It takes some combination of information about my body, and how it just moved, and any targets it hit, and so on —and gives back a number. The score is kind of upside-down, versus what you might expect: the lower the loss, the less I’m losing. My hand’s getting closer to the toy, and it’s getting there faster, and my brain spent less energy to do it…
Imagine we’re measuring the activity of some of my brain’s neurons, and writing down their history as a path in a state space. We can’t measure them all; if we’re lucky, maybe we measure 0.01% of them. The many dimensions of the space describe the firing rates of the neurons we’re measuring. At the same time, we score my behaviour with a loss function. We can insert that score as an extra dimension in the state space. In this state-plus-loss space, the added dimension becomes the direction of “up and down” — downhill means lower loss means better.
To reach my goal better, of course my neurons can’t just fire independently of each other, doing their own things as separate individuals. And not only should my neurons fire in some interdependent patterns, and follow some kind of coherent path — they should specifically follow paths in the state-plus-loss space that fall downhill to better performance.
The firing patterns that are described by downhill paths are the useful patterns, in terms of the score we’re keeping. They’re the patterns that are not only coherent, but more coherent with respect to my goal.
Your loss
That’s all fine, if a loss function is given. But when is it explicitly given? Can I maybe design it? What’s the best scoring method? Well, do I know what game I’m playing? What is my goal? That’s not just something unchanging that’s imposed on me.
My brain wasn’t born with a hard-coded list of all the tasks I’d ever have to perform and precise ways to score them.7 We start our lives as babies squirming and flailing, trying to figure out how to even move our limbs coherently. Months later, we might decide to reach for one toy rather than another. And as we continue to grow, our reaching gets increasingly complicated and abstract. Eventually, we might learn some mathematics.
In each moment, even when I’m not thinking about loss functions, I act like there’s something I’m trying to achieve — a score I’m trying to boost. My brain interprets my senses, channels my attention, creates my task. And it implicitly keeps score, even when I’m not explicitly quantifying anything.
The brain’s own score isn’t a single number that we’ve calculated separately and tacked onto some meager measurements of a fraction of the brain. A state-plus-loss space like the one mentioned earlier is just a poor imitation of some even larger state space describing everything about the brain8 — something scientists so far cannot measure.
Anyway, the kind of information we’d use for scoring an explicit loss function isn’t something that individual neurons generally have access to. They’re like birds who know things because they watch their immediate neighbours. Meanwhile, I know the things I know because I am the flock. I don’t see them, and they can’t see me.
And yet, as parts of the complete and complex physical process of the brain, my neurons fly together down the slopes of an energy landscape, where “energy” is the implicit loss I’m always trying to minimize.
We exist as we have survived, and survive as we have predicted.9 A goal is like a mismatch between prediction and reality, and downhill is the direction of impetus or behavioural gravity which best attempts to resolve the mismatch. Should we be surprised that downhill movement — goal-directed movement — inevitably emerges in living systems?
We survive as we have predicted, and predict as we have learned. All the parts of my brain are always trying to fall downhill together, but in doing so they also continue to refine and redefine what “downhill” even means. Baby’s first goal is flailing and squirming, which transforms into reaching and grasping, and later into planning and writing. I move down an energy landscape—but the landscape itself changes!
Anything that pushes me uphill even a little is something I wasn’t predicting. Call it a surprise, or a disturbance, or evidence. If I had already learned about it, I would’ve predicted it. “Downhill” would already factor it in. My plans would cancel it out, in effect. I wouldn’t have been diverted off the slope. A thing can’t surprise me if I already truly, deeply accept it!
… but what if I don’t?
Then when the surprise hits, it’ll nudge me uphill.
And then?
I learn. I hope.
Our tendencies, habits, or preferences are like valleys that are worn into the landscape of our behaviour. Channels into which we tend to fall into and flow, like a marble rolling into the nearest groove. These attractive areas of state space are conveniently called attractors.
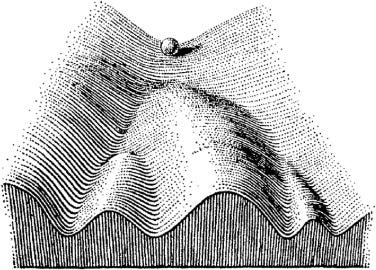
Flows in deeper, steeper valleys are more robust. When our path through the landscape is surrounded by high valley walls, then stronger forces need to interfere to push us over and out of the valley — and disrupt our habits. If we only get pushed halfway before the disturbance lets up, it’s easy to fall right back onto the path already followed.
So what’s stubbornness? It’s like a valley that keeps getting deeper and steeper; a region of the landscape that “refuses” to allow flows within it to be diverted, or for itself to be worn into some other shape, regardless of mounting evidence or disturbances.
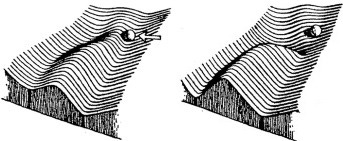
To change the world, you cannot be too willing to be changed by it.
Canalization is a concept which originated in genetics, to explain why phenotypes — for example that a fox looks like a fox, or that a bird nests its young in a particular way — may remain stable even when there are local disturbances, such as mutations in single genes, or changes in the weather.
Canalization is not about the mere presence of valleys or attractors, or else it's totally unoriginal. It's about the self-reinforcing nature of the process of channel-cutting or valley-eroding. It’s the tendency of the landscape to deepen and steepen. It’s attractorfication.
What if canalization is excessive? What if it keeps us captive, falling through our lives along the bottom of inescapable chasms of habit? What if a piece of critical evidence isn’t enough to nudge us over the walls of harmful normalcy? What if some large valley dominates the landscape, its many smaller branches or tributaries always pulling us in, no matter where we start? What if I never shut up?
Recent evidence hints at a “general factor of psychopathology”, conveniently called ‘p’.
If such a factor is real, and a reliable test shows I have more of it, then we’re more likely to observe that I have mental illness of any kind. Of course, whether I actually exhibit some mental illness or other still depends on the influence of specific hereditary or environmental factors — for example, being wealthy enough to experiment with therapies and experiences as it suits me.
Scott Alexander mentions that a general factor like ‘p’ is not the same as specific dependencies between disorders, where one condition tends to lead into another. He gives the example of developing an anxiety disorder because you're terrified of the demons you keep hallucinating. A general factor would increase the probability of both the anxiety disorder and the hallucinations, without requiring that one precedes or causes the other.
The 2023 paper “Canalization and plasticity in psychopathology” proposes that canalization is ‘p’.10
Our general theory states that: cognitive and behavioral phenotypes that are regarded as psychopathological, are canalized features of mind, brain, or behavior that have come to dominate an individual’s psychological11 state space. We propose that the canalized features develop as responses to adversity, distress, and dysphoria, and endure despite, rather than because of, evidence. We also propose that their depth of expression or entrenchment determines, to a large extent, the severity of the psychopathology, including its degree of treatment-resistance and susceptibility to relapse.
[…] we can imagine a valley as representing a cognitive or behavioral phenotype, feature, or ‘style’, and its depth and steepness is intended to encode its strength of expression, robustness, influence, and resilience to influence and change
(You should check out Scott's review of the paper for plenty more discussion.)
I find it hard to disagree with this. Anything we might define as mental illness and which was acquired through learning, may find its remedy through even more learning which shifts us away from the pathological pattern — so long as the pattern isn’t robust to the shift. It makes sense that regardless of the particular origin or character of a mental illness, it may persist when its dynamics are too robust.
Of course, the particular origin or character of a mental illness does still matter. I might say I learned a pattern that’s now so robust it’s hurting me—but which pattern is it, and where did I learn it? The paper spends some time exploring how canalization might matter to specific classes of mental disorders, for example those that are internalizing (e.g. depressive) versus externalizing (e.g. addictive).
A pattern judged to be too robust is called over-canalized. One of the canal paper’s authors is Karl Friston, the instigator of the recent formalism of active inference. So of course, the paper also frames over-canalization as predicting too hard:
Cast in Bayesian terms, the pathology we have chosen to highlight in this paper pertains to when the precision (or confidence) of prior beliefs (a prediction or model) becomes inappropriately high, leading to a failure of adaptability and the perpetuation of cognitive or behavioural entrenchment.
Over-canalization may be like pulling too long on a finger trap — while being caught in memories of situations where pulling had been a good way to free your fingers:
Moreover, apparently maladaptive phenotypes may initially have been adaptive for a given context - but critically, have become too entrenched, influential, and insensitive to new or changing conditions, i. e., they become, through canalization, insufficiently adaptive.
Canalization isn't inherently bad. We rely on “well-trodden paths” to make our way in the world. The answer to clenching cannot be to never contract any muscles again. We can view all tendencies or habits, even good ones, as channels in which we prefer to flow. For example, when performing familiar tasks we can often be very confident about the sequence of movements we need to make.
Given that you’ve started moving your leg to walk, you have a high prior (or an “extremely precise belief”) that you should bend your knee a certain way.
- Scott Alexander
Whether a behaviour is “too robust” depends on context.12 Here’s the tradeoff: the valleys in the landscape should be deep and steep and stable enough to keep up our good habits, but not so deep and steep and stable that new evidence or experiences can never push us over the walls of the valley, and begin to sculpt even better behaviour.
The right amount of compression pressure is not zero.
- Michael Edward Johnson
Hebb and flow
So far we’ve seen that:
Viewing a brain as a dynamical system, the paths the system follows in state space describe the overall patterns of “movement” of the brain’s parts—say, the firing rates of neurons over time; we could also call these paths the system’s flows.
The parts of living systems generally flow downhill on an energy landscape, improving a physical score which, if we could quantify it, would describe how well the system is achieving its implicit goals.
The shape of the energy landscape itself changes as part of this process—in other words, learning can occur and goals can change.
Valleys or steep areas in the landscape may tend to be self-reinforcing, and we call this tendency canalization. It keeps behaviour locally robust, and it may be either adaptive or dangerous, depending on what the behaviour is robust to.
Now: when we speak of valleys, we’re looking at an overall description of the state space of the brain or mind. That’s a top-down view of the whole forest — of the patterns that emerge because of the local actions of all the system’s parts. But what’s changing about those individual actions, that collectively results in canalization or robustening?
My brain wasn’t born with a hard-coded list of all the tasks I’d ever have to perform and precise methods to score them.
Memories and behaviours are things that gradually emerge from the coordination of my brain’s parts, as I interact and gather in the world.
Baby’s first goal is flailing and squirming, which transforms into reaching and grasping, and later into planning and writing.
Babies’ movements grow more coherent and complex, as their brains have ways to update the structure of their cells in light of the perceived success or failure of their movements to achieve certain results.
“I” operates at the level of goals, and the full machinery of my brain works out the little details.
Scientists have discovered a number of mechanisms that neurons use to adjust how they influence one another. One of these is Hebbian reinforcement, which the authors of the canal paper hold especially responsible for canalization.
Why?
The rough idea of Hebbian reinforcement is this: when one neuron (N1) fires and even slightly influences a next neuron (N2) to fire shortly afterward, the connection between them tends to be strengthened, so that N1 influences N2 more strongly in the future. N2 associates harder with N1 — it comes to fire more predictably with respect to N1.
When neurons fire more predictably with respect to each other, that implies a contraction of the landscape they move over. You don’t need a 100-dimensional landscape — 100 different changing numbers — to describe the path in state space that 100 neurons follow, when they all fire similarly. So Hebbian reinforcement leads to redundancy. At the extreme of redundancy, when all neurons are firing exactly the same way, we could describe them all at once by remembering just one number, over time.
Every single one of those damned birds is heading due east at the speed of light.
There are two related and crucial effects of Hebbian reinforcement. When a system of neurons is stimulated by novel information from outside the system — say, visual patterns from the eyes — that information will drive the patterns of N1-then-N2 firing in the system. While that’s happening, Hebbian reinforcement would contract the system onto firing patterns that reflect the structure of the information. In other words, the strengthening influences between neurons will reflect the strength of the associations in the sensory data. So the first crucial Hebbian effect is the acquisition of new patterns.
But we’re not concerned just with whether a pattern is present or absent, but with how present it is. A little Hebb can incept a pattern; a lotta Hebb can make sure it’s the only pattern around.13 So the second crucial Hebbian effect is that neurons obtain solidarity — they vibe14 more strongly.
For better or worse, it’s harder to disrupt a strongly shared vibe. This is our plainly-stated hypothesis about how the steepening of the valleys occurs: the steeper boundaries in state space reflect an increase in the coherence of the dynamics of the system, which is due to a mechanism that locally reinforces influences.
In parallel to redundancy, Hebbian reinforcement should also lead to exclusivity. If neurons A and B share a little of vibe X, we can reinforce vibe X between them. And if neurons C and D share a little of vibe Y, we can reinforce vibe Y. At the beginning, neuron A might have been able to influence neuron C with a bit of vibe X, and neuron C might have been able to influence neuron A with a bit of vibe Y. But as the A-B and C-D groups vibe more strongly on X and Y respectively, the members of each group become less likely to influence the members of the other. In fact, to maximally reinforce their own vibes, they should really try to suppress each other. So we might expect Hebbian reinforcement to partition (rather than mingle) a networked system, splitting it into self-reinforcing vibe cliques15 with exclusive dynamics.
These insights about redundancy and exclusivity are simple enough to apply to a small network — but what about a brain?
For example, some regions of my brain send down signals to my muscles through my spinal cord, to control my movements. What happens if different parts of those regions vibe among themselves in conflicting ways? I can’t take multiple, mutually exclusive actions — I can’t reach one of my hands to the right at the same time as I move it to the left. Brains have to solve this problem by selecting (at most) one of the exclusive alternatives16, or by finding a compromise when it makes sense to do so.17
Because of behavioural constraints like those, but also because of the particular architecture of the brain, we have to be careful when using our intuitions about Hebbian reinforcement to try to describe the relationship between neurons and behaviour. My brain’s entire state space isn’t a monolith that can split any which way into vibe cliques. The different dimensions of the space represent the different parts of my brain, and those parts aren’t all directly connected.18 The Hebbian mechanism acts locally between parts that are directly connected, and how its reinforcing effects spread through the network depends on the complexities (and oddities) of the actual architecture.19
The authors of the canal paper see Hebbian reinforcement as just one potential part of the mechanisms of canalization in the brain.
We speculate that the canalization could occur via (at least) three mechanisms: 1) an atrophy-related reduction in abundant synaptic connections, selectively sparing well-reinforced synapses and associated circuits, 2) top-down inhibition or neglect of specific circuitry (e.g., linked to traumatic memories), or 3) strong potentiation of selective synapses and circuits (Bliss, 1990). All scenarios should reduce freedom within the global system by biasing certain circuits or sub-states.
The potentiation or atrophy of the influences between neurons occurs through local mechanisms, but its relationship to behaviour emerges in larger-scale interactions across the brain. In a given circuit, Hebbian mechanisms may strengthen some vibes to dominate over others. But at a critical moment, maybe a circuit’s now-dominant vibe makes a cringey or dysphoric contribution to the larger negotiations playing out across the brain, and the entire circuit ends up inhibited by the processes that select non-conflicting behavioural alternatives. Is Hebbian reinforcement also at work in the selection machinery, to make this inhibition more robust? If it is, wouldn’t that be in opposition to what Hebbian reinforcement originally achieved in the now-inhibited circuit? If we’re interested in canalization at the level of behaviour, clearly we won’t always be able to associate it with a single Hebbian reinforcement event.
Exclusivity can play out in funny ways. One wrinkle in the system offsets another, and before long it’s wrinkles all the way down.
And should we be satisfied with that?
For everyone strives to keep his individuality as apart as possible, wishes to secure the greatest possible fullness of life for himself; but meantime all his efforts result not in attaining fullness of life but self-destruction, for instead of self-realisation he ends by arriving at complete solitude. All mankind in our age have split up into units, they all keep apart, each in his own groove; each one holds aloof, hides himself and hides what he has, from the rest, and he ends by being repelled by others and repelling them.
- Dostoevsky, The Brothers Karamazov
If you’re already familiar with loss functions, functional optimization, and energy landscapes, you could skip the intro.
However, given the confusion expressed by Scott Alexander (and some others in the comments) about the nature of energy landscapes, I thought I ought to make this post more accessible to people who aren’t already experts in dynamical systems or machine learning.
Our greatest successes are in physics, I think. An electron is clearly an electron, even when we frame it as a potential smearing through a physical field. And as far as I know, we don’t know of a way to transform or decompose an electron into something else.
On the other hand, higher-order objects like molecules and birds and governments have the habit of losing their identities before too long.
Roughly: a superorganism is to organisms what an organism is to cells.
Of course, this is only a rough analogy. The life of a single cell inside a multicellular organism isn’t identical to the life of an organism inside a flock or society.
This isn’t directly analogous to the bird flocking example, where each of the birds is moving through physical space, and as a result the entire flock is also moving through physical space.
My neurons are more or less stationary inside my brain, but they “move” in the state space of activity depending on how they are firing — and as a result, my body literally moves through physical space. Certain “movements” in the space of neural activity become signals to my muscles, where the firing of neurons is converted to literal movements.
Some neuroscientists might contend that our simplification would be a little closer to reality if it described the state of each neuron as just a yes-no answer: is this neuron currently firing, or not? Then a single point in state space would be a list of which neurons are currently firing, and a path in state space would be a history of firing events for all neurons.
Sure, we could do that. But it would still be a simplification.
Anyway, we’ll be able to expand our reasoning later. We can imagine dynamical systems built out of whichever variables we end up liking.
A machine learning researcher might say that we’re born with the biological equivalent of inductive biases that enable us to learn to learn all sorts of tasks more easily. But we should be careful to ask how those inductive biases came to evolve — and assuming we could explicitly capture them as mathematics, whether they would look anything like the kinds of inductive biases and meta-learning algorithms designed by researchers.
And possibly some other stuff too — namely the full state of the sensory and motor organs, if we’re following the free energy principle.
A free energy expert might say that “free energy doesn’t entail life, life entails free energy”. In other words, minimizing free energy is no guarantee of surviving; but surviving means that you must have minimized free energy. Have I neglected this distinction?
Our model rests, to a large extent, on the legitimacy of ‘p’ and thus, we refer the interested reader to the original text that introduced the notion (Caspi et al., 2014) - as well as other appraisals (Levin-Aspenson et al., 2021; Kelley et al., 2019; Lahey et al., 2012; van Bork et al., 2017) and supportive evidence (Selzam et al., 2018; Brainstorm et al., 2018; Goodkind et al., 2015; Sha et al., 2019; Elliott et al., 2018; Barch, 2017; Menon, 2011; Patalay et al., 2015).
The authors speak of a psychological state space. We are allowed to speak of the mind as a dynamical system, just like the brain. Which parts of the mind are stable long enough measure them? Thoughts? This is an empirical challenge.
Of course there are also difficulties in measuring the brain, but I’ve stuck with describing the brain rather than the mind, since I think it serves at least as well for my purpose of illustration.
Ultimately, we probably want to describe them both, and learn how they relate.
Here’s an example from biology of good canalization: every cell in your body has the same genetic material, give or take some mutations and viral editing across your lifetime. However, cells from different tissues (e.g. your liver versus your heart) look and act differently because they use the same genetic material differently. Different tissues correspond to different attractor states that a stem cell can fall into. It’s important that your tissues are robust to changing their identity — the attractors should be very self-reinforcing. When this fails and cells rebel from their tissues, you get cancer.
There is a little bit of contention over whether it’s more appropriate to call it Hebbian learning, or Hebbian plasticity, or something else. If we use plasticity to refer to anything that can alter the influences between parts of the brain, which depends on those influences being changeable (plastic), then of course Hebbian mechanisms should be called plasticity mechanisms.
However, the authors of the canal paper rightly point out that the changes wrought by Hebbian mechanisms can harden the system against further changes, so that in a sense they are anti-plastic mechanisms. And maybe we could raise a similar objection to calling it Hebbian learning.
I like Hebbian reinforcement. It’s more precise. Hebbian contraction seems good too, though I’ve not seen it used before.
In the case of neurons, a shared “vibe” might look like similar oscillations in their firing rates. Vibes shared by people are obviously more complicated.
The traditional term is cell assembly, and Hebbian theory is sometimes also called cell assembly theory.
It’d be more appropriate to say that the brain needs to globally attract to an implementable behavioural state, rather than that it necessarily starts with discrete alternatives and then must select between them.
A popular (e.g. 1, 2, 3) class of models proposes that behavioural selection occurs in feedback loops between the thalamus and cortex, modulated by the basal ganglia. A far too simple rendition of this is that 1) the cortex is a general-purpose learner, which supports a vast array of locally specialized-but-flexible dynamics across its huge area, 2) the thalamus is a kind of hub of information integration, which — in massively parallel feedback with cortex—synergizes with the most relevant sensory data, to shape the flexible cortical dynamics into candidate attractors, 3) the basal ganglia implement some kind of reinforcement learning that preferences and promotes some of these “thalamo-cortical” attractors over others, up to the point that movement may be produced.
Similarly, the brain doesn’t equally activate Hebbian mechanisms in all of its systems at all times. Some systems (or even individual neurons) have roles in which it makes sense for them to contract and acquire new patterns, while others ought to keep their influences more stable.

